How To Find Vapor Pressure Of A Solution
| RAOULT'S LAW AND Not-VOLATILE SOLUTES This folio deals with Raoult's Constabulary and how information technology applies to solutions in which the solute is non-volatile - for case, a solution of salt in water. A non-volatile solute (the salt, for example) hasn't got any tendency to grade a vapour at the temperature of the solution. It goes on to explain how the resulting lowering of vapour pressure affects the boiling betoken and freezing betoken of the solution. | |
| Important:If you haven't already read the page about saturated vapour pressure, you should follow this link earlier you go on. Apply the Dorsum push button on your browser to render to this page when yous are ready. | |
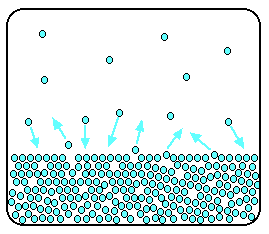
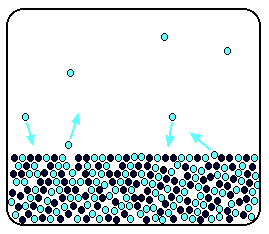
| Raoult's Law In that location are several ways of stating Raoult'due south Law, and you tend to use slightly unlike versions depending on the situation you are talking most. You can utilise the simplified definition in the box beneath in the case of a single volatile liquid (the solvent) and a non-volatile solute. The vapour force per unit area of a solution of a non-volatile solute is equal to the vapour pressure of the pure solvent at that temperature multiplied past its mole fraction. In equation form, this reads: In this equation, Po is the vapour pressure of the pure solvent at a item temperature. xsolv is the mole fraction of the solvent. That is exactly what it says it is - the fraction of the total number of moles present which is solvent. You summate this using: Suppose you had a solution containing 10 moles of water and 0.1 moles of sugar. The total number of moles is therefore 10.i The mole fraction of the water is: A simple caption of why Raoult's Police works There are two means of explaining why Raoult'due south Police force works - a simple visual way, and a more sophisticated fashion based on entropy. Because of the level I am aiming at, I'm just going to look at the simple way. Think that saturated vapour pressure is what you lot go when a liquid is in a sealed container. An equilibrium is prepare where the number of particles breaking away from the surface is exactly the aforementioned as the number sticking on to the surface again. Now suppose yous added enough solute so that the solvent molecules simply occupied 50% of the surface of the solution. A certain fraction of the solvent molecules will have enough energy to escape from the surface (say, 1 in thousand or i in a million, or whatever). If you reduce the number of solvent molecules on the surface, you are going to reduce the number which tin can escape in any given time. But it won't make any divergence to the ability of molecules in the vapour to stick to the surface again. If a solvent molecule in the vapour hits a bit of surface occupied past the solute particles, it may well stick. There are apparently attractions between solvent and solute otherwise you wouldn't have a solution in the first place. The net effect of this is that when equilibrium is established, there will exist fewer solvent molecules in the vapour phase - it is less likely that they are going to break away, but there isn't any problem about them returning. If in that location are fewer particles in the vapour at equilibrium, the saturated vapour pressure is lower. Limitations on Raoult'south Law Raoult's Constabulary only works for ideal solutions . An ideal solution is divers as 1 which obeys Raoult's Law. Features of an ideal solution In practice, there's no such thing! However, very dilute solutions obey Raoult's Law to a reasonable approximation. The solution in the last diagram wouldn't actually obey Raoult'southward Law - it is far too concentrated. I had to describe it that concentrated to brand the point more conspicuously. In an ideal solution, it takes exactly the same amount of energy for a solvent molecule to break abroad from the surface of the solution as it did in the pure solvent. The forces of attraction betwixt solvent and solute are exactly the same equally betwixt the original solvent molecules - not a very probable effect! Suppose that in the pure solvent, 1 in chiliad molecules had plenty energy to overcome the intermolecular forces and break away from the surface in any given fourth dimension. In an ideal solution, that would notwithstanding be exactly the aforementioned proportion. Fewer would, of course, break away because in that location are now fewer solvent molecules on the surface - but of those that are on the surface, the aforementioned proportion even so break away. If there were strong solvent-solute attractions, this proportion may be reduced to 1 in 2000, or ane in 5000 or whatever. In any existent solution of, say, a salt in water, there are strong attractions between the water molecules and the ions. That would tend to tedious down the loss of water molecules from the surface. Yet, if the solution is sufficiently dilute, there will be skilful-sized regions on the surface where you still have water molecules on their ain. The solution will so approach ideal behaviour. The nature of the solute There is another affair that you have to be careful of if you are going to do any calculations on Raoult's Police force (beyond the scope of this site). You may take noticed in the little calculation about mole fraction farther upwards the page, that I used sugar equally a solute rather than common salt. There was a good reason for that! What matters isn't really the number of moles of substance that y'all put into the solution, but the number of moles of particles formed. For each mole of sodium chloride dissolved, you get 1 mole of sodium ions and ane mole of chloride ions - in other words, yous get twice the number of moles of particles as of original common salt. So, if y'all added 0.1 moles of sodium chloride, there would actually be 0.2 moles of particles in the solution - and that's the effigy you would have to utilize in the mole fraction adding. Unless you think carefully nigh it, Raoult'southward Police only works for solutes which don't modify their nature when they dissolve. For example, they mustn't ionise or associate (in other words, if yous put in substance A, it mustn't form Atwo in solution). If it does either of these things, you have to treat Raoult's police with groovy intendance. | |
| Note:This isn't a problem you are likely to have to worry virtually if you are a UK A level student. Just be enlightened that the problem exists. | |
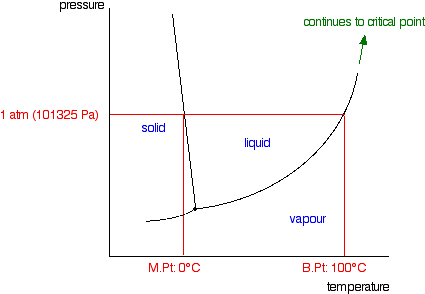
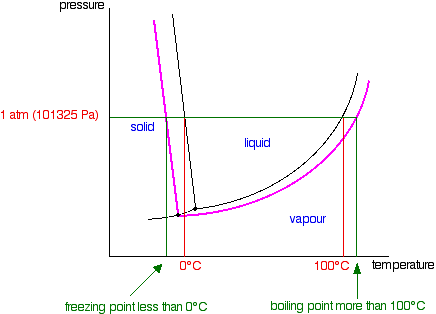
| Raoult's Constabulary and melting and humid points The effect of Raoult'south Law is that the saturated vapour pressure of a solution is going to be lower than that of the pure solvent at any particular temperature. That has important effects on the phase diagram of the solvent. The next diagram shows the phase diagram for pure water in the region around its normal melting and boiling points. The one atmosphere line shows the weather condition for measuring the normal melting and boiling points. | |
| Notation:In common with most phase diagrams, this is fatigued highly distorted in society to show more clearly what is going on. If y'all haven't already read my page about phase diagrams for pure substances, you lot should follow this link before y'all become on to brand proper sense of what comes next. Use the Dorsum push on your browser to render to this folio when you are gear up. | |
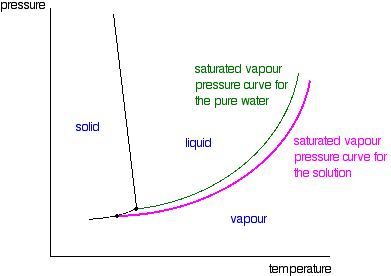
| The line separating the liquid and vapour regions is the set of atmospheric condition where liquid and vapour are in equilibrium. Information technology can be thought of as the effect of force per unit area on the humid point of the water, just information technology is also the bend showing the effect of temperature on the saturated vapour pressure of the h2o. These two means of looking at the same line are discussed briefly in a note most half-style down the page most stage diagrams (follow the last link above). If y'all draw the saturated vapour pressure bend for a solution of a non-volatile solute in water, information technology volition always be lower than the curve for the pure h2o. | |
| Note:The curves for the pure water and for the solution are often fatigued parallel to each other. That has got to exist wrong! Suppose y'all take a solution where the mole fraction of the water is 0.99 and the vapour force per unit area of the pure h2o at that temperature is 100 kPa. The vapour pressure of the solution volition be 99 kPa - a fall of 1 kPa. At a lower temperature, where the vapour pressure of the pure water is ten kPa, the fall will simply be 0.1 kPa. For the curves to exist parallel the falls would have to exist the aforementioned over the whole temperature range. They aren't! | |
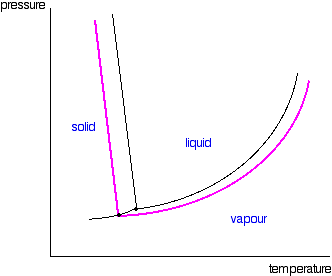
| If you await closely at the last diagram, y'all will see that the point at which the liquid-vapour equilibrium curve meets the solid-vapour curve has moved. That point is the triple point of the system - a unique prepare of temperature and pressure conditions at which it is possible to get solid, liquid and vapour all in equilibrium with each other at the same fourth dimension. Since the triple point has solid-liquid equilibrium present (amongst other equilibria), information technology is also a melting signal of the system - although not the normal melting indicate because the pressure isn't 1 atmosphere. That must mean that the phase diagram needs a new melting signal line (a solid-liquid equilibrium line) passing through the new triple point. That is shown in the adjacent diagram. Now we are finally in a position to see what upshot a non-volatile solute has on the melting and freezing points of the solution. Expect at what happens when y'all draw in the 1 atmosphere pressure line which lets you measure the melting and boiling points. The diagram also includes the melting and boiling points of the pure h2o from the original phase diagram for pure water (black lines). Because of the changes to the phase diagram, you tin see that:
We have looked at this with water as the solvent, but using a different solvent would make no difference to the argument or the conclusions. The just departure is in the slope of the solid-liquid equilibrium lines. For most solvents, these slope forrard whereas the h2o line slopes backwards. Yous could bear witness to yourself that that doesn't affect what we have been looking at by re-drawing all these diagrams with the slope of that detail line changed. Yous will notice information technology makes no difference whatsoever.
To the phase equilibrium card . . . To the Physical Chemistry menu . . . To Main Menu . . . © Jim Clark 2004 (modified Jan 2014) | |
Source: https://www.chemguide.co.uk/physical/phaseeqia/raoultnonvol.html
Posted by: haysaidd1989.blogspot.com

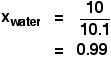
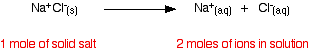

0 Response to "How To Find Vapor Pressure Of A Solution"
Post a Comment