How To Find Log Inverse In Scientific Calculator

Log Estimator
Anti-Log Computer
| Number ∓ Base | Amount |
|---|---|
| Enter the number(to the power of x) | |
| Select the Base of operations value | |
| Antilog Result | Amount |
|---|---|
| Antilog value |
Mathematical Formulas
Calculating log (logbten):
logbx = y implies by = x.
Where,
- b = base of operations,
- y = number,
- x = log value.
Calculating Antilog:
y = 10x
Where,
- 10 = number,
- y = antilog value.
Logarithms and Anti-Logarithms: How It Works and Its Significance
- Guide Authored by Corin B. Arenas, published on October 1, 2019
If you've ever wondered how experts determine keen distances, earthquake intensity, and global economic growth rates, and then you've come to the right place.
Calculating very large sums tin can be ho-hum and confusing. But with the help of logarithms (log) and antilogarithms (antilog), calculations tin exist made simpler.
Read on to learn more about log and antilog, how they work, and why these are relevant mathematical concepts.
What is Logarithm?

A logarithm is the power to which a number (referred to every bit the base) must be multiplied to itself to obtain a given number. In simpler terms, logarithm solves the problem:
How many times practise we multiply b to obtain another number y?
Logarithm counts the number of times the same gene must be multiplied to make it at a given number.
Who Came Up with Information technology?
Log was invented in the 16th century as a calculation tool by Scottish mathematician, physicist and astronomer, John Napier. He wrote the volume Mirifici Logarithmorum Canonis Descriptio with tables and numbers discussing natural logarithms, laying downwardly the background for its basic concept.
Napier coined the term logarithm from the Greek word logos which ways 'ratio or proportion,' and arithmos which ways 'number.' When combined, it literally ways 'ratio number.'
2 Types of Logarithms
The natural logarithm of a number is its log to the base of the constant due east, where eastward is approximately equal to 2.718281828459. The equation is written as log east (x).
If a logarithm does not specify a base, similar this example: log(thousand), it's known every bit a common logarithm that uses the base 10.
log(1000), it'south known as a common logarithm that uses the base 10.
How is Log Used?

Once y'all start calculating figures past millions, billions and trillions, it tin get quite taxing. Whether it concerns counting a lot of money, the growth of populations, or covering large distances, log can work for you. It can simplify large sums that involve long and confusing equations, making them easier to grasp.
Here is the standard equation for log:
logb(x) = y
Where,
- The number multiplied to itself (b) is the base.
- The number of times information technology is multiplied (y) is the logarithm.
- The number obtained (x) is written in the parenthesis.
To understand how the concept works, hither'due south an example with a smaller number:
Question: How many 2s do we multiply to get 32?
b = 2, x = 32
log2(32) = y
Reply: 2 x ii 10 2 ten 2 x 2 = 32
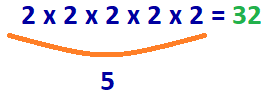
5 number 2s must be multiplied to obtain the number 32.
The answer: logtwo(32) = 5
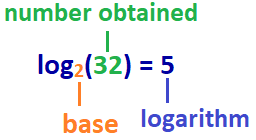
Therefore, in this example: The logarithm of 32 with base ii is 5, or log base 2 of 32 is 5.
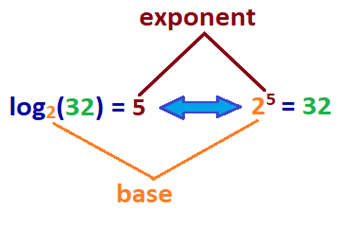
Moreover, log is the inverse function of exponentiation, where the mathematical performance is written every bit bn. b is the base that is multiplied according to the power of n, which is the number of times information technology is multiplied to itself.
What does this mean? The log of a number is the exponent to which base b is multiplied to obtain a given number. To give you lot a better idea, refer to the sample log equation set alongside its exponential equation below.
| log | exponent |
|---|---|
| log2(32) = 5 | 2v = 32 |
Now allow's try it with a large number.
Question: How many 10s practise we multiply to go 150,000,000,000?
b = x, ten = 150,000,000,000
logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.1760912590557
This is solved by using the log office in a scientific computer. Or use the estimator on this page to get the answer.
How is Antilogarithm Related to Log?

A log number tin then be returned to its original number. This tin be done using antilogarithm (antilog). Thus, the antilog is the inverse part of log. Likewise, antilog functions to exponentiate a simplified log value.
To compute the antilog of a number y, yous must raise the logarithm base of operations b (normally x, sometimes the abiding e) to the power that will generate the number y.
Hither is the equation for antilog using base ten:
tenx = y
Where x is the exponent and y is the antilog value.
For example, if nosotros take this equation, log(5) = x, its antilog will be 10x = five.
- Log: log(five) = 0.698970004336019
- Antilog: ten0.698970004336019 = 5
Now allow'southward endeavour information technology with a larger number.
If we take log(150,000,000,000) = 10, its antilog will be 10x = 150,000,000,000.
- Log: logten(150,000,000,000) = xi.1760912590557
- Antilog: 10xi.1760912590557= 150,000,000,000
Importance and Real-World Applications

Prior to the invention of calculators, logarithms were used to simplify computations in various fields of knowledge, such as navigation, surveying, astronomy, and later on, engineering.
Imagine sailing in the middle of nowhere in the 16th century. Navigators back then relied on the position of stars and a sextant mechanism to pinpoint their exact location. Without modern technology to assistance you compute great distances, yous can use log to simplify your calculations. Accuracy is important, or you risk more days at sea with meager supplies. Fewer equations hateful less room for mistake.
What about other practical applications? Alive Scientific discipline states logarithms relate geometric progressions to arithmetic progressions. If yous've e'er noticed repetitive shapes and patterns in nature, architecture, and art, these formations possess their own corresponding logarithmic values.
Today, knowledge from how these patterns piece of work influences the way humanity constructs and designs houses, buildings, and urban landscapes.
Logarithms are too used to limited the extent and intensity of certain scales. Apart from wide distances, and high speeds, it measures other things such as:
- Audio intensity
- Audio frequency
- Force of windstorms
- Strength of earthquakes
- Corrosive level of acids
- Hardness of minerals
- Effulgence of stars
Permit's take decibels as an case. To make speakers louder by 10 decibels, it must exist supplied by x times the power. Every bit you increase it to +20 dB, it will need 100 times the power, and past +30 dB it will demand 1,000 the power.
Moreover, audio intensity progresses arithmetically. It besides changes proportionally with the logarithm of a sound moving ridge which progresses geometrically.
Below is a table from Live Scientific discipline listing different logarithmic scales with their respective linear scales.
| Field of Measurement | Linear Scale | Logarithmic Calibration |
|---|---|---|
| Sound Intensity | Power (×10) | Decibels (dB) (+10) |
| Note Pitch | Frequency (×2) | Note (+12 half steps) |
| Brightness of Star | Power per unit area (×100) | Magnitude (-5) |
| Earthquake Intensity | Energy (×1000) | Richter Calibration (+2) |
| Air current Intensity | Current of air speed (×one.5) | Beaufort Scale (+1) |
| Mineral Hardness | Absolute hardness (×iii approx.) | Mohs Calibration (+1) |
| Acidity or Basicity | Concentration of H+ions (×10) | pH (-1) |
In Measuring Rates and Ranks

Co-ordinate to Kalid Azad, the math educator backside BetterExplained.com, logarithms are how we figure out how fast something is growing.
Common logarithms basically draw numbers in terms of their powers of 10. When information technology comes to interest rate, the logarithm is the growth in an investment.
In determining the GDP growth rate of a state, analysts review GDP in subsequent years. They take the Gross domestic product of the previous year, and the Gross domestic product the following twelvemonth, and then compute the logarithm to discover the estimated growth charge per unit.
Search engines use the link graph to help score the importance, trustworthiness & authority of documents across the web. Google's PageRank was a major evolution in search which boosted search relevancy and helped Google search marketshare.
According to Azad, in a scale of 1 to 10, a landing page with a PageRank of 2 is 10 times more popular than a page with a PageRank of i. If a site has a PageRank of 5, and a competitor site has a PageRank of ix, and then it has a difference of 4 orders of magnitude.
An society of magnitude ways roughly a 10x deviation, or a ranking is 1 digit larger compared to the other. In this case, a site with a PageRank ix is 100,000,000 more popular than a site with PageRank 1.
The Bottom Line
Log and antilog are significant computing methods that allow us to simplify large sums. Simplifying shortens the computation process and makes calculations easier to grasp. This helps reduce room for error.
Moreover, using log provides measurable scales for gauging natural phenomenon, similar earthquake intensity, the force of windstorms, and the brightness of stars. In terms of finance, logarithms let us to pinpoint interest rates and economic growth rates.
It's practically used in many fields. Big values that depend on the accuracy of measurement benefit from using logarithmic calculations.
Nearly the Author
Corin is an ardent researcher and writer of financial topics—studying economic trends, how they affect populations, equally well every bit how to aid consumers make wiser financial decisions. Her other feature articles can be read on Inquirer.internet and Manileno.com. She holds a Master's degree in Creative Writing from the University of the Philippines, one of the top bookish institutions in the world, and a Bachelor'south in Communication Arts from Miriam College.
Source: https://www.calculators.org/math/log-antilog.php
Posted by: haysaidd1989.blogspot.com


0 Response to "How To Find Log Inverse In Scientific Calculator"
Post a Comment